---

\[\newcommand{\bra}[1]{\left\langle{#1}\right\vert } \newcommand{\ket}[1]{\left\vert {#1}\right\rangle} \newcommand{\braket}[2]{\left\langle {#1} \, \middle\vert \,{#2} \right\rangle } \newcommand{\d}{\mathrm{d}} \newcommand{\R}{\mathbb{R}} \newcommand{\C}{\mathbb{C}} \newcommand{\K}{\mathbb{K}} \newcommand{\D}[2]{\frac{\d {#1}}{\d {#2} }} \newcommand{\Partial}[2]{\frac{\partial {#1} }{\partial {#2} }} \newcommand{\op}{\hat} \newcommand{\uvec}{\hat} \newcommand{\dfdas}{:=} \newcommand{\Eqn}[1]{\text{(Eqn. }\ref{#1}\text{)}} \newcommand{\vard}{\mathfrak{d}} \newcommand{\vare}{\mathfrak{e}} \newcommand{\e}{\mathrm{e}} \newcommand{\i}{\mathrm{i}} \newcommand{\norm}[1]{\left\vert{#1}\right\vert} \newcommand{\set}[1]{\left\lbrace {#1}\right\rbrace} \newcommand{\comm}[2]{\left[ #1 , \, #2 \right]} \newcommand{\slot}{\,\cdot\,} \newcommand{\lact}{\triangleright} \newcommand{\ract}{\triangleleft} \newcommand{\vac}{1\!\!\!\mathsf{\phantom{I}I}} \newcommand{\la}{\mathfrak} \notag\]

This post contains debates inside my mind, after failing to write it concisely in plain paragraphs, I decided to write this post in the form of three characters, Smarty, Dummy and Sassydiscussing. Some of the cited materials are selected to prove a point, but may contain more information than the speaker intended or conveyed.

Can you build a QC using Stern-Gerlach Experiment?

---

Smarty: Quantum computing is quite complicated and can be hard to understand. If I make use of electrons in a Stern-Gerlach experiment as qubits and gates. like this:

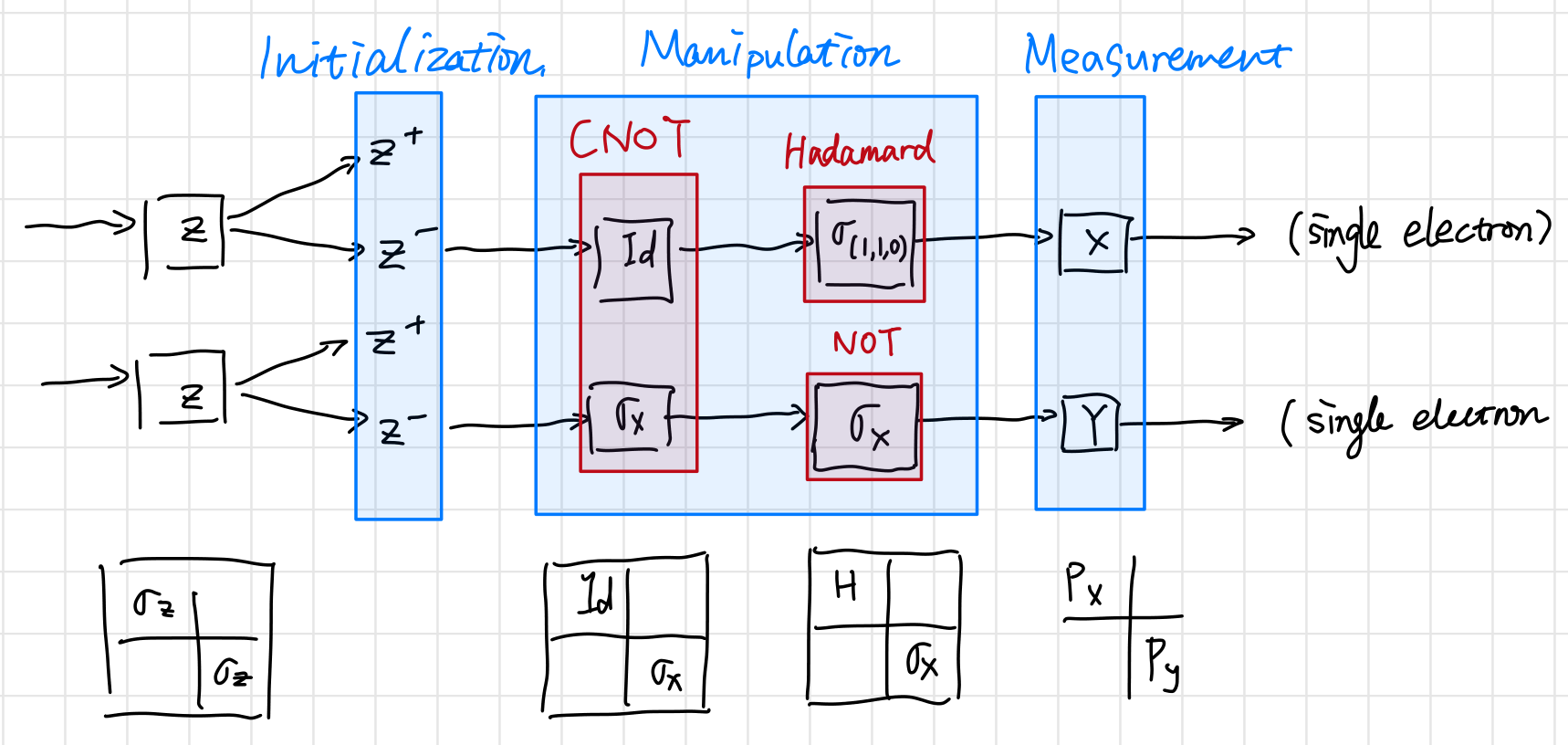
Then it will be very intuitive for me and the reader!

---

Dummy: Then why hasn’t anyone done so? This is perfect for heuristic educations as well as actual commercial/ experimental setups. Yet I looked up on the internet, but no one seemed to have made such construction. The only paper I found is about an implementation using Mach Zehnder Interferometer¹ (see table 3. about how each gate is implemented).

---

Sassy: Hmm… while you guys are making your diagram, I am wondering how this computer works. You know, when you draw some diagram like that, you give an input, and an output is generated. How is that anything “quantum”? I mean, I could easily write any quantum circuit down and know the answer, without even running the actual machine.

---

Dummy: And wait! The above CNOT gate does not flip the second spin with respect to the first spin’s orientation.

---

Smarty: Of course! You guys are right! A CU gate (controlled gate) is meant for creating entanglement. The above CNOT gate does not create any entanglement.

---

Dummy: And fixing that would partly explain Sassy’s problem. An entangled state can create superposition and thus cause uncertainty. You will then get a different result for each measurement, like in Glover’s Algorithm, where you get the matching result with almost 100% chance. But you are still not 100% sure that is it.

---

Smarty: Ok, that’s easy. I’ll just measure the total spin of two spins. That should create a maximally-entangled state. Let me try something…

---

Sassy: But you guys haven’t answered my question yet. Even if you came up with something like that, this circuit is still predictable, and thus deterministic. * writes on the note *

---

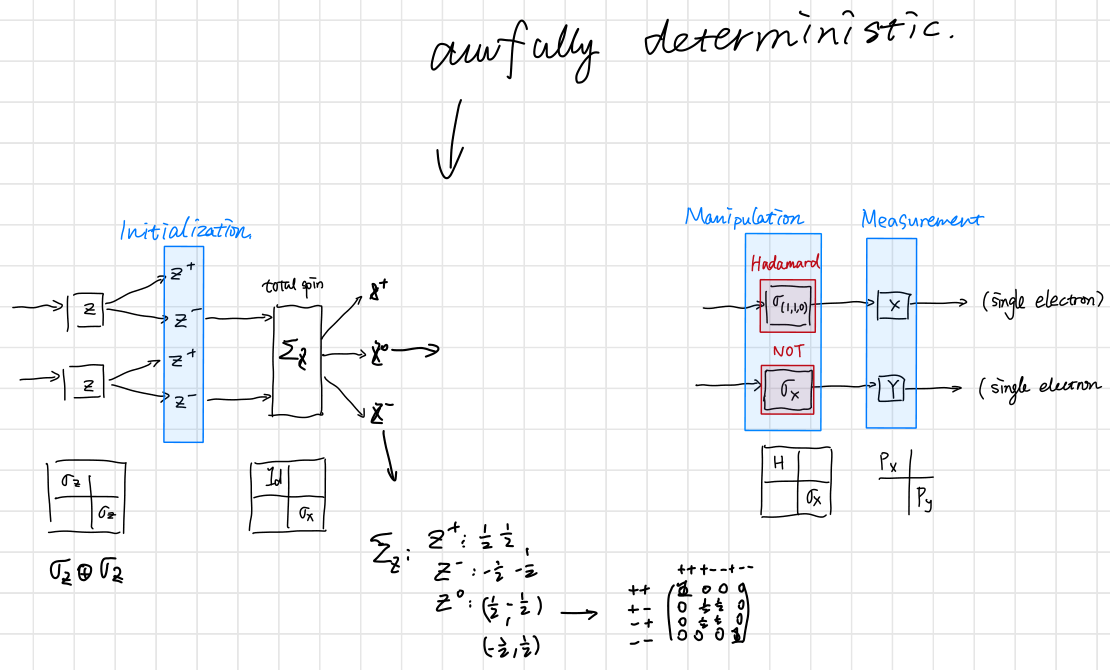
Smarty: Okay, I seem to get stuck on this one.

---

Dummy: Yeah, you are… see if you implement the above “circuit”, if that’s one, you will end up with a matrix (call that $\Sigma_Z$):

\[\Sigma_Z=\begin{pmatrix} 1 &&&\\ & \tfrac{1}{2} & \tfrac{1}{2} & \\ & \tfrac{1}{2} & \tfrac{1}{2} & \\ &&& 1 \end{pmatrix}.\]

But $\Sigma_Z$ is not even an unitary matrix!

---

Smarty: Oh I know! The apparatuses used in Stern-Gerlach is in fact apparatuses for measurement. A measurement is in no way represented by a unitary matrix.

In fact, those matrices shown in the diagram are not even $\sigma$ matrices, rather projection operators, such as

\[P_\uparrow =\ket{\uparrow}\bra{\uparrow}=\begin{pmatrix}1&0\\0&0\end{pmatrix}.\]

Thus my attempt to build a quantum computer using Stern-Gerlach experiment is bound to fail! That’s why no one has done that before!

---

Dummy: Wow! Can’t believe how we missed that!

---

Are QC deterministic? Can We Simulate QC Using Classical Computers?

---

Sassy: But I am still wondering, even if you are working with a true quantum computer, like that bluemix in IBM, or other pioneer sites like quantumplayground, when you draw a circuit, the outcome is still pretty clear to me. I can look at any circuit and tell you what the outcome would be. You wouldn’t need any quantum computers to do that. You just need a well-trained quantum programmer!

---

Smarty: Sassy’s got a point. A program or a “code” should be deterministic, when you read a code, the steps should be clear, and ideally, can be carried out by “human computers”. And IBM and other big companies are even providing “coding languages” for quantum computers, like Qiskit and Q#. And many more languages!

As a rule-of-thumb, if a human could manually describe or imagine how something ought to operate, that imagining can be implemented on a Turing machine. Quantum computers fall into this category. (from SE)

How is that possible?

---

Dummy: I agree with you guys. Remember quantum computers are just about solving evolutionary equations? You can even get your desired output by simply multiplying the matrices! You don’t even need a code to do that!

---

Smarty: Dummy and Sassy inspired me. I looked up the internet and found out that in principle, you can do that. For $n$-qubits’ simulation, the unitary matrix of a quantum gate would be $2^n\times 2^n$, which is a HUGE number.

• $n=30$ you will need at least $2^{33}=8GB$ of RAM. A publicly-accessible laptop is capable of doing it, but an old computer may not have a sufficient amount of RAM.

• $n=40$ you will need at least $2^{43}=8TB$ of RAM. This is definitely out of reach for publicly-accessible things, you will need access to a computing server.

• $n=50$ you will need at least $2^{53}=8PB$ of RAM. Some top-tier super-computers “only” have $2.8PB$ of RAM.

  (from SE)

So our way of simulating a quantum computer will not work.

---

Dummy: So that’s why people are saying quantum computers are efficient! I guess I didn’t fully understand the meaning and implications that statement of yk-liu’s first post about “quantum computers are exponentially faster than classical computers” since qubits runs “in parallel”.

---

Is Simulation of QC/TQC at Hardware Level a Way to Quantum Supremacy?

---

Sassy: But what if the simulation is at the hardware level?

I could calculate various properties of a given material using ab-initio calculations. Does that mean I could simulate the hardware of a quantum computer to circumvent the exponential cost of memory?

For a QC, like that bluemix in IBM, or, I could calculate the qubit’s state of the junction.

Or like topological quantum computers (TQC)? Like in many papers, a TQC is implemented by chemical potentials, domain walls or defects in topological insulators. A braiding is a (slow) change of the environment. That does not require those memories!

Worst case, I could build a toy model for QC or TQC, and run the simulation in a classical computer. This seems to circumvent the exponential cost of memory. Since

1. No matter how many qubits you are using, you need linearly more “virtual material” to simulate for these qubits to reside on.
2. No matter how many quantum gates you are using, you need linearly more “time” to calculate the result.

This will give us a computer that runs quantum code as fast as a quantum computer, meaning “cost linearly in resources proportional to that of a quantum computer”. Is this possible?

---

Sassy: If this is true, this could mean quantum supremacy! All you need then, is a specially tailored computer that runs ab-initio calculations really fast, and you run the calculations on that “simulation”, and you will have a classical computer You can factorize any prime number, as large as you want! RSA encryption will be rendered obsolete!

There is even a code on GitHub called QTop. The claim of the program is that:

QTop allows for the simulation of topologies with arbitrary code depth, qudit dimension, and error models. Currently, QTop features Kitaev quantum double models, as well as color codes in 3-regular planar tilings.

---

Dummy: Guys, that’s quite a rosy picture, but I would like to ask one more time. Why hasn’t anyone done that yet?

I found that for TQC, it indeed can be simulated in polynomial time in a classical computer. (Chapter 4.3. Clifford Operators in paper²).

I followed the paper and found Van den Nest’s paper³, you will see that a certain class of non-trivial quantum circuits, called “Clifford circuits”, can be simulated efficiently on a classical computer, and can hence not provide any speed-up w.r.t. classical computation.

But sadly, quantum circuits that involve only Clifford group operations are not universal for quantum computing. In fact, one can efficiently simulate such circuits on a classical computer.

• A Clifford circuit is any quantum circuit which is composed of Hadamard, PHASE and CNOT gates.

• Difference between Clifford gates and universal gates? Cn together with any other gate not in Cn form a universal set of quantum gates⁴

---

Smarty: I am skeptical about Sassy’s Point. I think it has been theoretically proven that QC (with T-gate) will out perform CC. Yet I could not find a way to disproof your proposal.

And Dummy made a very good point. So what I was wondering have already been proven by the paper in such an abstract level: you don’t even need to consider which type of QC you are using (be that QC or TQC), classical simulation can only utilize Clifford gates, which is not capable of performing arbitrary quantum algorithms. Thus quantum computers are indeed more capable than a computer.

==what can/connot be done with only Clifford gates? Shor? Grover?== Couldn’t find any real world algorithms.

---

A Small Misconception about Quantum Code

---

Dummy: You actually got me thinking. Forget the simulation of an actual implementation of a QC, and consider the quantum code itself. The quantum code itself is still a code. Does that mean I could write a program on a classical computer that read these quantum code and give a result in reasonably short time?

---

Smarty: Let me address Dummy’s statement first. I am no computer scientist, but I know for sure such program will not be able to give the result for any code in polynomial time. In other words, it will not provide a drastic improvement over speed or resource benefits.

Let’s consider a classical computer for now. If there exists such program, which I will call magical program™, such program will give result in polynomial time for any well-optimized code. Or you would have proven $P=NP$ (wiki link), which is generally considered not true. Consider a well-optimized code A for factoring large prime numbers. If you input code A to your magical program™, it can do nothing better than running code A itself, or you would have cracked RSA by now.

Although it is not possible to improve any program that runs $\exp (n^3)$ to polynomial time, I don’t know if you can make minor improvement to it so it will run a bit faster, like from $\exp (n^3)$ to $\exp (n^2)$. Also, a complier can sometimes make small optimization to your code, such as the Intel fortran compiler. But such improvement are routine, tends to modify more on a technical, machine-specific level rather than algorithm level, and are not always prominent or even possible. Therefore, if you do have such magical program™ that automagically applies to any type of codes and improve the speed, you would be famous.

But I don’t know any proof why such programs do not exist. My take on this subject is that it is hard even to do that with a classical code, let alone a quantum one. So Dummy’s magical program™ might not exist.

---

Sassy: By the way, your question is related to mine in Chapter 1:Can you build a QC using Stern-Gerlach Experiment? And I think a program that reads other program and gives an output is related to the halting problem.

---

Complexity?

From the computational complexity stand point, QC can only solve of BQP problems. NP-hard problems are still out of reach.

Maybe a direct improvement on computational power is a way with a further perspective to go?

As a wild thought: are there more ways to realize a “computer” theoretically? can or cannot a complete paradigm shifting computer be realized? No? Turing machine dictates that all “computers” by definition is reduced to our “computer”?

To be continued.

---