---

\[\newcommand{\bra}[1]{\left\langle{#1}\right\vert } \newcommand{\ket}[1]{\left\vert {#1}\right\rangle} \newcommand{\braket}[2]{\left\langle {#1} \, \middle\vert \,{#2} \right\rangle } \newcommand{\d}{\mathrm{d}} \newcommand{\R}{\mathbb{R}} \newcommand{\C}{\mathbb{C}} \newcommand{\K}{\mathbb{K}} \newcommand{\D}[2]{\frac{\d {#1}}{\d {#2} }} \newcommand{\Partial}[2]{\frac{\partial {#1} }{\partial {#2} }} \newcommand{\op}{\hat} \newcommand{\uvec}{\hat} \newcommand{\dfdas}{:=} \newcommand{\Eqn}[1]{\text{(Eqn. }\ref{#1}\text{)}} \newcommand{\vard}{\mathfrak{d}} \newcommand{\vare}{\mathfrak{e}} \newcommand{\e}{\mathrm{e}} \newcommand{\i}{\mathrm{i}} \newcommand{\norm}[1]{\left\vert{#1}\right\vert} \newcommand{\set}[1]{\left\lbrace {#1}\right\rbrace} \newcommand{\comm}[2]{\left[ #1 , \, #2 \right]} \newcommand{\slot}{\,\cdot\,} \newcommand{\lact}{\triangleright} \newcommand{\ract}{\triangleleft} \newcommand{\id}{1\!\!\!\mathsf{\phantom{I}I}} \newcommand{\la}{\mathfrak} \notag\]

Generators in Mathematics

From the last post, a one-to-one correspondence between three entities has been established, namely

• Left-invariant vector field $X$, such $X$ is sometimes called the infinitesimal generator of the one-parameter group $t \rightarrow \exp(tX)$.
• Tangent vector at identity $X_e\in T_eG$,
• One-parameter subgroup $\gamma_X(t)$.

The relationship between them can be summarized as

graph LR
A(Xe)-->|Translated around G|B(Left-invariant vector field)
B-->|Integral|C(one-parameter subgroup)
A-->|Exponential Map|C

Lie Group’s Generator

A connected Lie group is generated by any neighborhood of identity.

Proof: (from G Bellam)

1. Recall that $G$ is connected implies that the only non-empty closed and open subset of $G$ is $G$ itself. The proof is done by showing the neighborhood generates a set $H$ that is both open and closed.
2. Since the inversion map $i:g\mapsto g^{-1}$ is smooth, for an open set $U$, the inverse $U^{-1}\dfdas \set{g^{-1}\mid g\in U}$ is open in $G$. The intersection $U\cap U^{-1}$ is also open. It’s non-empty since $e\in U\cap U^{-1}$. Take $V=U \cap U^{-1}$.
3. If $g\in V$ then $gV=\set{gh\mid h\in U}$ is also open in $G$. Thus the set $V\cdot V \dfdas \bigcup_{g\in V} gV$ is also open in $G$. By induction, $H=V^n\dfdas\set{\prod_{i=1}^n g_i\mid g_i\in V}$ is open. $H$ is s subgroup of $G$ since it satisfies the four group multiplication rules. Moreover, $V$ is a subset of $H$.
4. We now show that $H$ is closed by contradiction.
5. Suppose $H$ is not closed, then there is a nonempty boundary of $H$, namely there exists $g\in \partial H \dfdas \overline H\backslash H$, $g\notin H$. Since $gV$ contains $g$, $gV\cap\partial H\neq\varnothing$. $V$ is also open, and when an open set intersect with a boundary $\partial H$, it must intersect with the interior (open set has no boundary to be “tangent to $\partial H$”). Thus $gV \cap H \neq \varnothing$.
6. Choose $h\in gV\cap H$. Since $h\in gV$, $h$ can be expressed as $h=gu, \ u\in V \subset H$. For $V\subset H$, $h=gu\in H$. Since the inverse map is closed in $V$, $u^{-1} \in V \subset H$. Since $H$ is closed, $h, u^{-1} \in H$, $hu^{-1} = g \in H$. But we assumed $g\notin H$, a contradiction.
7. Thus $H$ is both open and closed. $H=G$. Since $H$ is generated by the neighborhood of $e$, so is $G$.

This theorem can be understood as generating the real number $(\R,+)$. Take an arbitrarily small open neighborhood $(-\varepsilon, \varepsilon)$ of identity $0$, the entire $\R$ can be generated by adding $\varepsilon$ to itself to get $2\varepsilon$ and to $\infty$, or to add $-\varepsilon$ to $-\varepsilon$ to get $-2\varepsilon$ and to $-\infty$. But if the neighborhood does not contain both positive and negative numbers, say $(\varepsilon ,2\varepsilon), \ \varepsilon >0$, then you cannot get to $-\infty$. Therefore we require the set to not only contain $0$ but to be open, so there is always a negative number sitting next to $0$.

One important observation is that such neighborhood does not have any limitation on size. It can be arbitrarily small. How small can this neighborhood be?

Tangent Space and Neighborhood Diffeomorphism

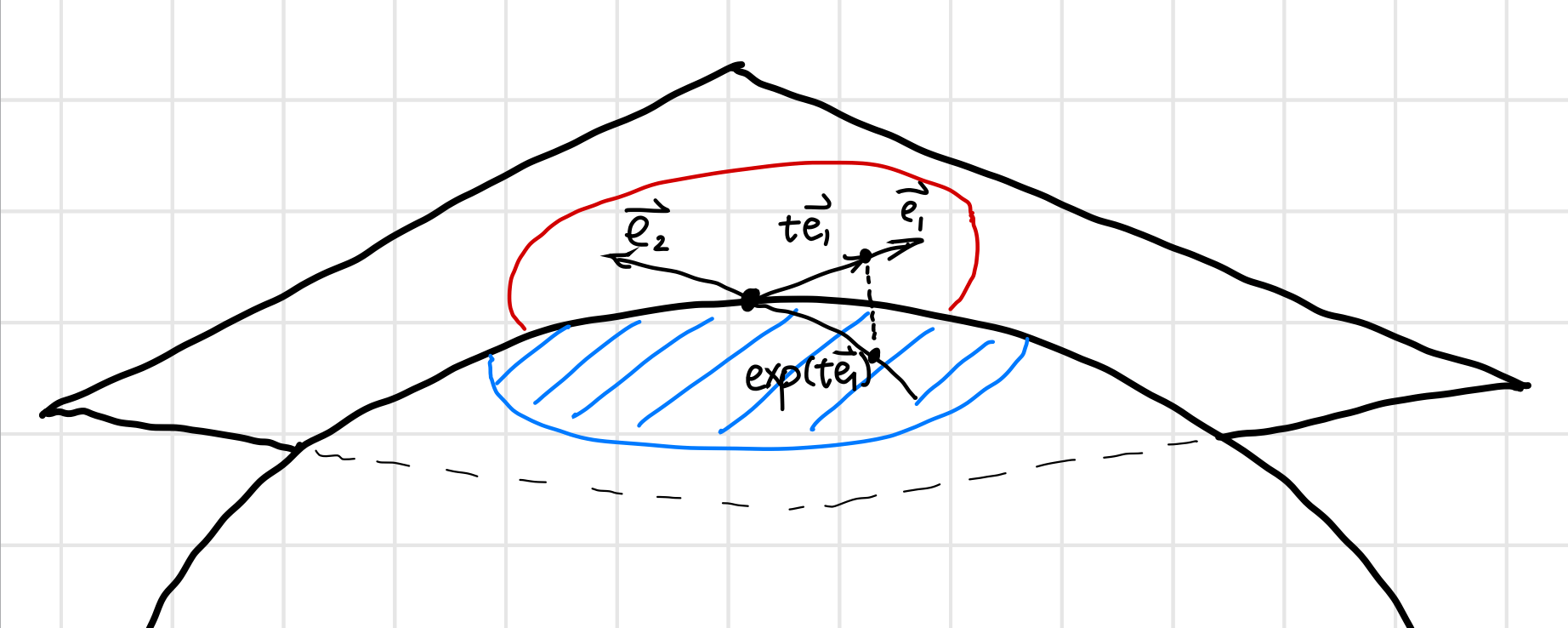
Taking smaller and smaller neighborhoods of e, one eventually “arrives” at the tangent space of $G$ at $e$. Namely, the tangent space $T_eG$ generates the entire Lie group.

To prove the above statement, we can prove that there is a diffeomorphism between an open neighborhood of tangent space and an open neighborhood near the identity.

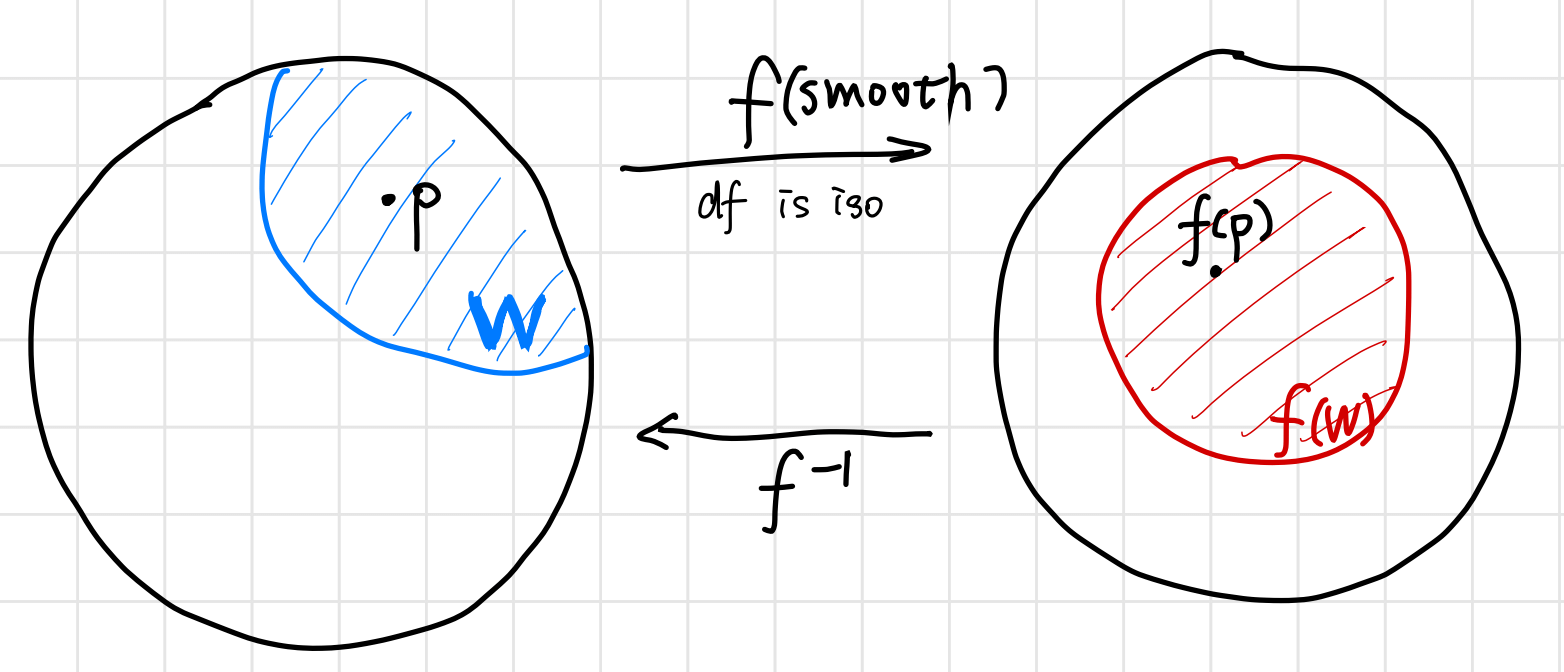
Proposition: The exponential map $\exp : T_e G \rightarrow G$ is smooth, and it is a local diffeomorphism at $0$.

Proof:

1. Inverse Function Theorem: Let $f : M \rightarrow N$ be a smooth map between two smooth manifolds $M$, $N$, and let $p \in M$ and $q = f(p)$. If $\d f_p : T_pM \rightarrow T_qN$ is an isomorphism, then there exists an open neighborhood $W$ of $p$ such that $f(W)$ is an open neighborhood of $q$ and $f$ restricts to a diffeomorphism from $W$ onto $f(W)$. In other words, a function is invertible in a neighborhood of a point in its domain as long as its derivative is continuous and non-zero at the point. Thus this function induces a diffeomorphism.

1. Since $\exp(tX) = \phi_X(t)$ is a curve on $G$, it’s tangent vector at $t=0$ is $X$, we have $\left.\D{}{t} \exp(tX) \right\vert_{t=0}=X$. This means that the map $\d \exp$ at $t=0$ is just identity map, which clearly has inverse. By the Inverse function theorem, $\exp$ is a local diffeomorphism.

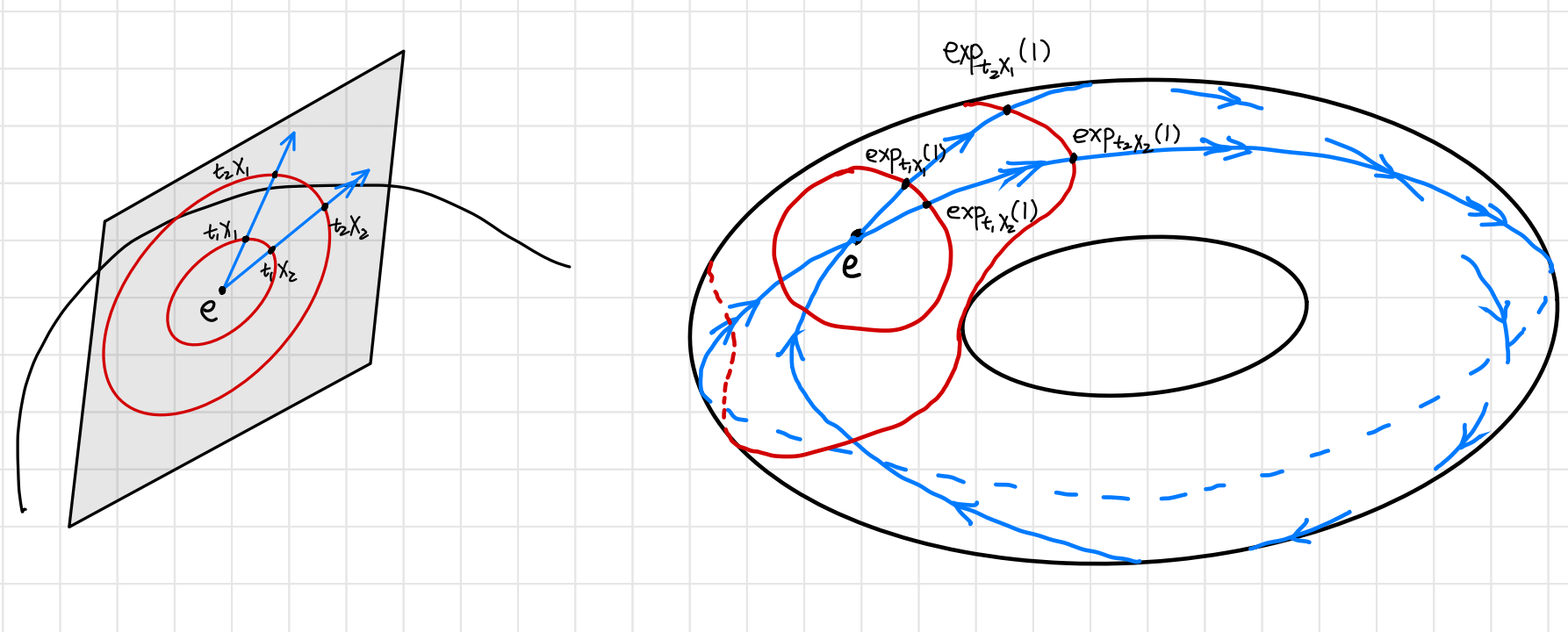
Tangent Space Encodes (Generates) the Lie Group

From the last two sections, the tangent space at $e$ is diffeomorphic to an open set $U_e$ of identity, which generates the entire Lie group. In this sense, the tangent space does generate the entire Lie group (that is compact and connected).

I like to think it as tangent vectors dictates different one-parameter subgroups which in turn “covers” the entire Lie group. Since the tangent space is in general uncountable, such is “cover” on a higher dimensional “surface” (or “volume”) using a lower dimensional “line”.

Associated Lie Algebra of Lie Group

Lie algebra should “know” everything about $G$, then it should know about the group operation, which leads to the Campbell-Baker-Hausdorff formula. (Tony Feng) The formula can be better understood with the “bracket” in Lie algebra is introduced as a measure of non-commutativity.

Lie published an article titled “Über Gruppen von Transformationen” in 1874. As early as 1871, the idea of an infinitesimal generator of a one-parameter group of transformations had already appeared in his work.

This point of view was essential to Emmy Noether’s 1918 article in the Göttinger Nachrichten establishing the relationship between symmetries of a variational problem and conservation laws. About ten years later, Noether published a very important article situating the representation theory of finite groups and of algebras in the context of noncommutative rings

The set of infinitesimal generators of one-parameter subgroups of a continuous group forms what today is called a “Lie algebra.”(This name was suggested much later by Weyl in his 1933–1934 lectures at the Institute for Advanced Study in Princeton.)

(from [Yvette])

General Lie Algebra

A Lie Algebra $\la g$ over a field $\K$ is a vector space over $\K$ (usually $\R$ or $\C$) equipped with a bilinear map called the Lie bracket:

\[\la g \times \la g \rightarrow \la g, \ \ (a,b)\mapsto \comm{a}{b}\]

such that

1. Skew-symmetric $[a, a] = 0$ for all $a \in \la g$.
2. Jacobian Identity $[a, [b, c]] + [b, [c, a]] + [c, [a, b]] = 0, \forall a, b, c \in\la g$.

Associated Lie Algebra

In the last post, the bracket of left invariant vector fields are defined. The brackets satisfies all the requirements of a Lie algebra. Hence, All left-invariant vector fields form a Lie algebra.

$\log$ Map, BCH formula

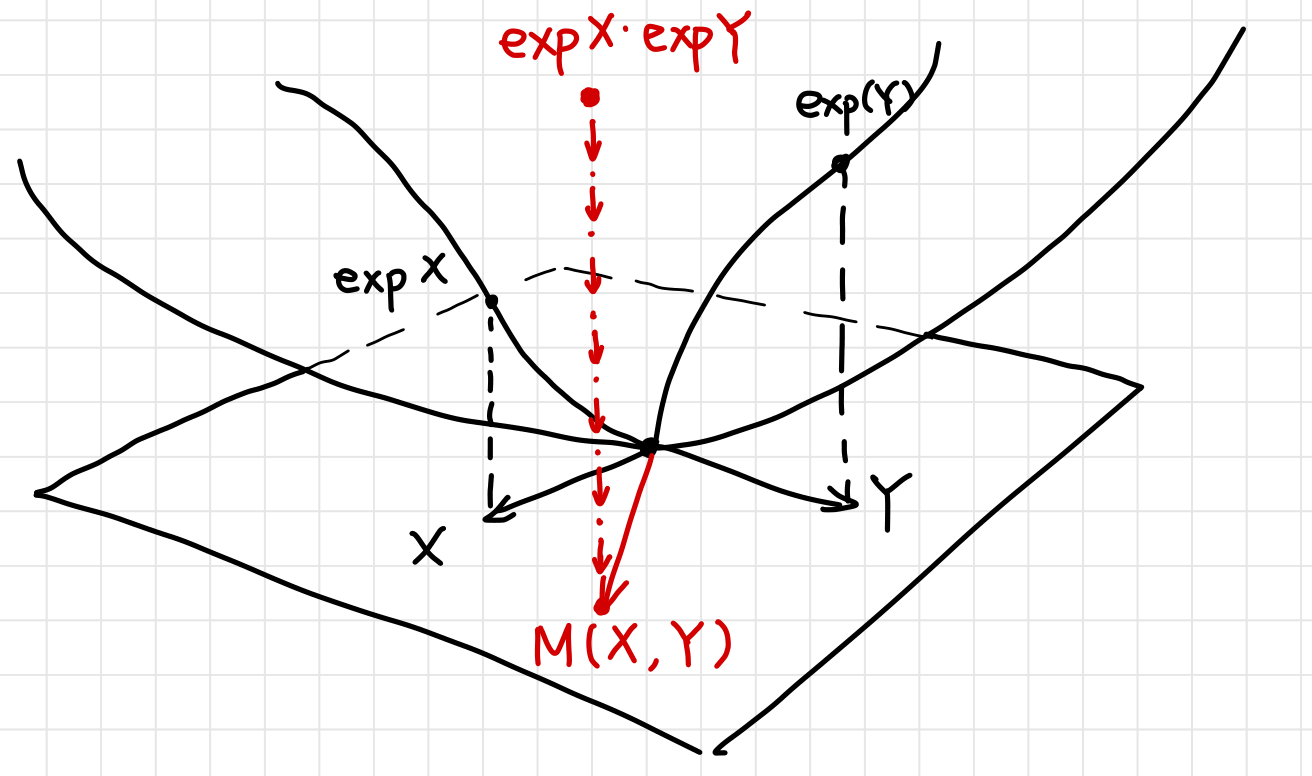
With $\exp$ map defined, $\log$ map arises naturally. Such $\log$ map is often described in the form of BCH formula.

\[\begin{align*} &e^X e^Y=e^Z\\ &Z=X+Y+\tfrac{1}{2}\comm{X}{Y},\quad \comm{X}{\comm{X}{Y}}=\comm{Y}{\comm{X}{Y}}=0\\ &\Rightarrow Z=\log (e^X e^Y) \end{align*}\]

Proof: see Math SO.